Free Movies Van Mario Sallieri

INFORMATION AND APPROACH OF EXCEPTIONS TO THE LAW GAUSS

The classical formulation of electromagnetism corresponds to Maxwell's laws, which consists of 4 equations. One of these equations, considered the Gauss law for magnetism says

The magnetic field integral to the "long" of a space any closed surface is 0.

That

can be expressed mathematically as follows:

and can be illustrated by the following image:

which show that for every closed surface S, the magnetic field lines enter on the surface is identical to that sale.


EMERGENCY APPROACH

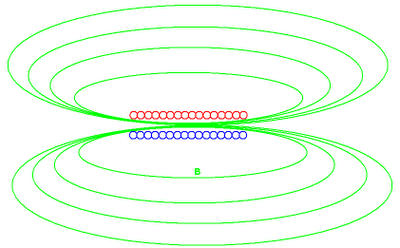
Suppose we have a solenoid, the magnetic field will be as follows:

In general relativity it is possible to define an event horizon around a mass compact enough (Black holes), so that no country can pass from inside to outside the event horizon. (In this theory gravity is considered curvature of spacetime, and able to permeate the event horizon).

of a solenoid oriented towards an event horizon, part of the magnetic field lines from crossing the event horizon, unable to return through it. Thus the event horizon would appear by itself an exception to the Gauss law for magnetism.

Moreover suppose that is placed at the ends of the solenoid two event horizons, with the intention that these horizons "suck" the magnetic field and to obtain a magnetic field distribution of the following type:

So that would get an exception to the law of Gauss different event horizon and a set that could operate as a magnetic monopole.

TRANSMISSION FIELDS: The crux of the matter

In theory the magnetic field at a point is defined by a vector that obeys the following formulation:

And what happens at that point does not depend on what happens in other parts of space where there are moving charges, ie the proximity of an event horizon does not affect you, or any barrier that does not involve charges moving. Thus the figure of the solenoid would be as follows:

In theory, a magnetic field have to propagate in the sense that you have to do a tour like a squirrel does which goes on for hazelnuts, and less in the direction you point the lines of force. The only legitimate seems to accept that a disturbance is recorded with a delay at a point away, being able to perhaps raise some experiment (the coil between two event horizons) to make a decision on whether there is traffic or not.

A similar approach can be made to the Gauss law of electrostatics.